ReMoE- Fully Differentiable Mixture-of-Experts with ReLU Routing

Paper: arXiv
Authors: Ziteng Wang, Jianfei Chen, Jun Zhu

Overview

Classical MoE with softmax and top-K gating mechanism suffer from non-differentiability (due to top-K being a non-differentiable function) which makes them difficult to train. This paper completely replaces softmax and top-K with ReLU. A router using ReLU selects the experts. ReLU naturally zeros all the negative activations, and the experts corresponsing to positive activations are chosen for the forward pass (explained more formally later). Authors use clever load balancing and sparsity loss to make sure the router has desired properties.

Preliminaries

Throughout this post: ${\mathbf{x}}^l=({\mathbf{x}}_t^l{)}_{t=1}^T\in {\mathbb{R}}^{T\times d}$, where $\text{T}$ is the total number of tokens (context length) and $\text{d}$ is the dimension of residual stream (d_model)

MoE

$$y_t^l=\sum _{e=1}^{E}R({\mathbf{x}}_t^l{)}_e{\text{FFN}}_e({\mathbf{x}}_t^l;d_{ffn})$$

$y_t^l$: This represents the output vector at layer $\text{l}$ for the token at position $\text{t}$. It’s the result of the MoE layer’s computation.

${\mathbf{x}}_t^l$: This is the input vector to the MoE layer at layer l for the token at position t.

$R({\mathbf{x}}_t^l{)}_e$: The subscript $\text{e}$ indicates the routing weight or importance assigned by the router to the e-th expert for the current input ${\mathbf{x}}_t^l$. The router essentially determines to what extent each expert should contribute to the final output.

${\text{FFN}}_e({\mathbf{x}}_t^l;d_{ffn})$: This represents the e-th Feed-Forward Network (FFN) expert. $d_{ffn}$ is the intermediate size of expert. Usually 4 * $\text{d}$.

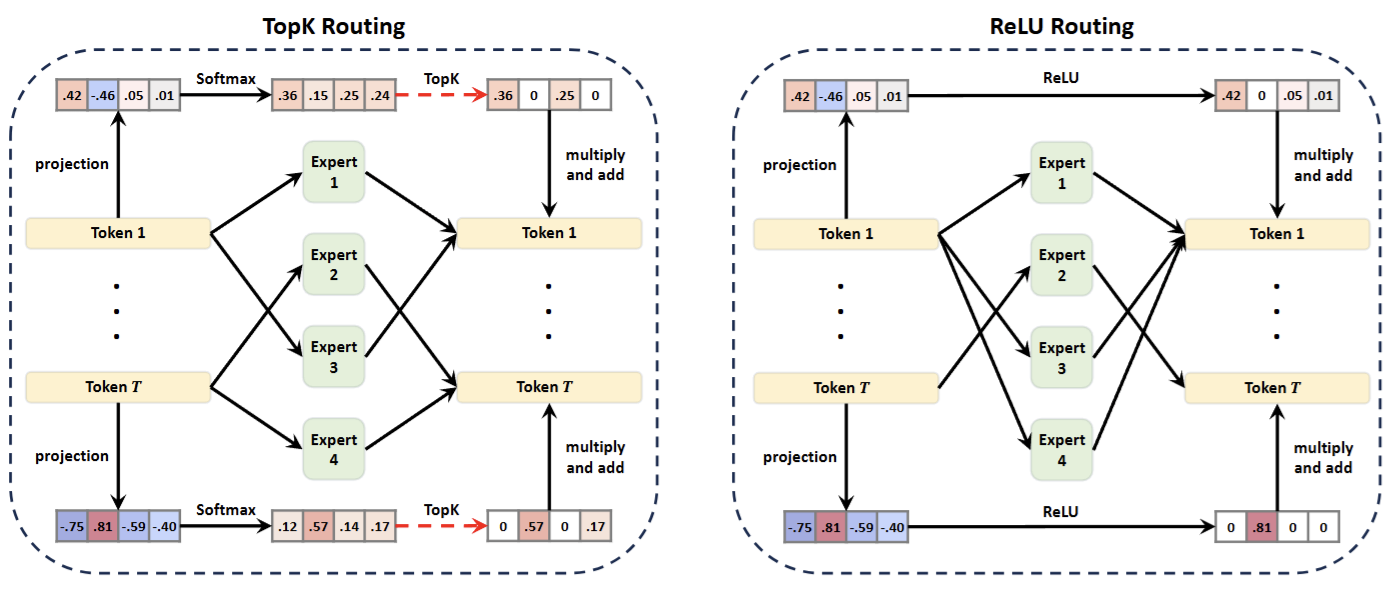
Top-K Routing

In Top-K routing the router is defined as:

$$R({\mathbf{x}}_t^l)=\text{Topk}(\text{Softmax}({\mathbf{x}}_t^l{\mathbf{W}}_r),k)$$

$({\mathbf{x}}_t^l{\mathbf{W}}_r)\in {\mathbb{R}}^{T\times E}$ and $\text{Top-k}$ retains the top $\text{k}$ values while setting the rest to zero.

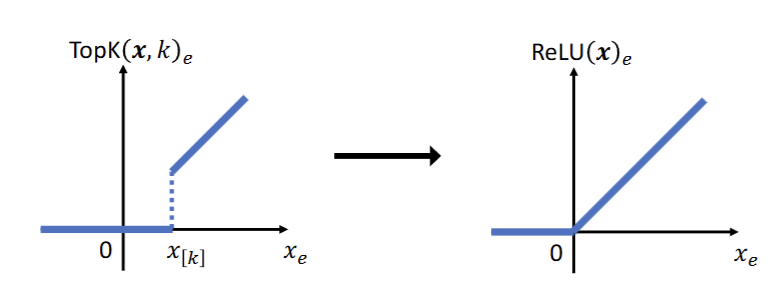
But the problem with top-K function is that it is clearly discontinuous with jump discontuity at the $\text{k-th}$ largest value as seen in the figure. The jump discontinuity can be fully eliminated with a ReLU and experts transition between being active and inactive at $0$.

ReMoE

ReLU routing function is defined as:

$$R({\mathbf{x}}_t^l)=\text{ReLU}({\mathbf{x}}_t^l{\mathbf{W}}_r)$$

$R({\mathbf{x}}_t^l)\in {\mathbb{R}}^{T\times E}$, with $(1-\frac{k}{E})$ being the sparsity where k is the number of active experts.
In regular $\text{Top-k}$ the Softmax outputs sum to 1, representing the probabilities of selecting each expert. Only the $\text{K}$ highest are retained and the rest are eliminated. But in $\text{ReMoE}$, $\text{ReLU}$ naturally acts as a gate at the point zero. The outputs of $\text{ReLU}$ routers represent the weights assigned to each expert, which can include 0. $\text{ReLU}$ allows the router to learn which experts to activate (i.e., when to produce 0s) in a fully differentiable manner.

Another key difference between them is that $\text{Top-k}$ is always forced to choose $\text{k}$ experts, but $\text{ReLU}$ can dynamically choose the number of experts as it’s not hard coded. This would possibly allow more compute to be dedicated to tokens which are difficult to process.

But the key question is how do we regulate the sparsity and load balance between experts?

Controlling Sparsity via $L_1$ regularization

To regulate sparsity and achieve the desired sparsity of $(1-\frac{k}{E})$, authors introduce a $L_1$ regularization loss along with the $L_m$ language modeling loss.

$$\mathcal{L}={\mathcal{L}}_{lm}+{\lambda }_i{\mathcal{L}}_{reg}$$

where,

$${\lambda }_{i+1}={\lambda }_i\cdot {\alpha }^{sign((1-\frac{k}{E})-S_i)}$$

${\lambda }_0$ and $\alpha$ are hyperparameters chosen at the beginning and from then ${\lambda }_{i+1}$ is adaptively changed at every step.

$S_i$ denotes average sparsity of all router outputs at step $\text{i}$,

$$S_i=1-\frac{1}{LTE}\sum _{l=1}^L\sum _{t=1}^T\sum _{e=1}^{E}1\{R(x_t^l{)}_e>0\}$$

The key intuition being, $\text{LTE}$ is the total number of experts that can be active for a forward pass, it’s the maximum possible number.
${\sum }_{l=1}^L{\sum }_{t=1}^T{\sum }_{e=1}^{E}1\{R(x_t^l{)}_e>0\}$ is the actual number of active experts in the forward pass.

$\frac{1}{LTE}{\sum }_{l=1}^L{\sum }_{t=1}^T{\sum }_{e=1}^{E}1\{R(x_t^l{)}_e>0\}$ gives us the ratio of $\frac{\#\text{active experts}}{\text{max number of experts}}$. So $S_i$ denotes the average sparsity.

Back to ${\lambda }_{i+1}$,
$sign((1-\frac{k}{E})-S_i)$ is positive if desired sparsity is lesser than $S_i$ (there are more active experts than desired). And ${\lambda }_{i+1}$ is increased by a factor of $\alpha$.
Similarly, if $sign((1-\frac{k}{E})-S_i)$ is negative if desired sparsity is greater than $S_i$ (there are less experts active than desired). So ${\lambda }_{i+1}$ is reduced by a factor of $\alpha$.

The regularization term ${\mathcal{L}}_{reg}$ uses the $L_1$-norm:

$${\mathcal{L}}_{reg}=\frac{1}{LT}\sum _{l=1}^L\sum _{t=1}^T||R(x_t^l)|{|}_1=\frac{1}{LT}\sum _{l=1}^L\sum _{t=1}^T\sum _{e=1}^{E}R(x_t^l{)}_e$$

With this ${\mathcal{L}}_{reg}$, we can control the sparsity around the desired level of $(1-\frac{k}{E})$. A key implication of this is that, on average, ReMoE ensures tokens are routed to $\text{k}$ experts across different layers, tokens maintaining same FLOPs as regular $\text{Top-k}$. So the model has complete control of how many experts to activate as long as the number of experts activated on average are within the desired level. We get to see the number of experts active across different layers varies.

Integrating Load Balancing into $L_1$ Regularization

To address load balancing, authors modify the loss term introduced above.

$${\mathcal{L}}_{reg,lb}=\frac{1}{LT}\sum _{l=1}^L\sum _{t=1}^T\sum _{e=1}^E{f}_{l,e}R(x_t^l{)}_e$$ $$f_{l,e}=\frac{E}{kT}\sum _{t=1}^{T}1\{R(x_t^l{)}_e>0\}$$

$f_{l,e}$ is non-differentiable and represents the average activation ratio of expert $\text{e}$ in layer $\text{l}$,relative to the desired ratio $\frac{k}{E}$. This mechanism penalizes experts receiving more tokens by driving their router outputs toward zero more rapidly.

Three Stages of training of ReMoE

Authors observe three stages during training.

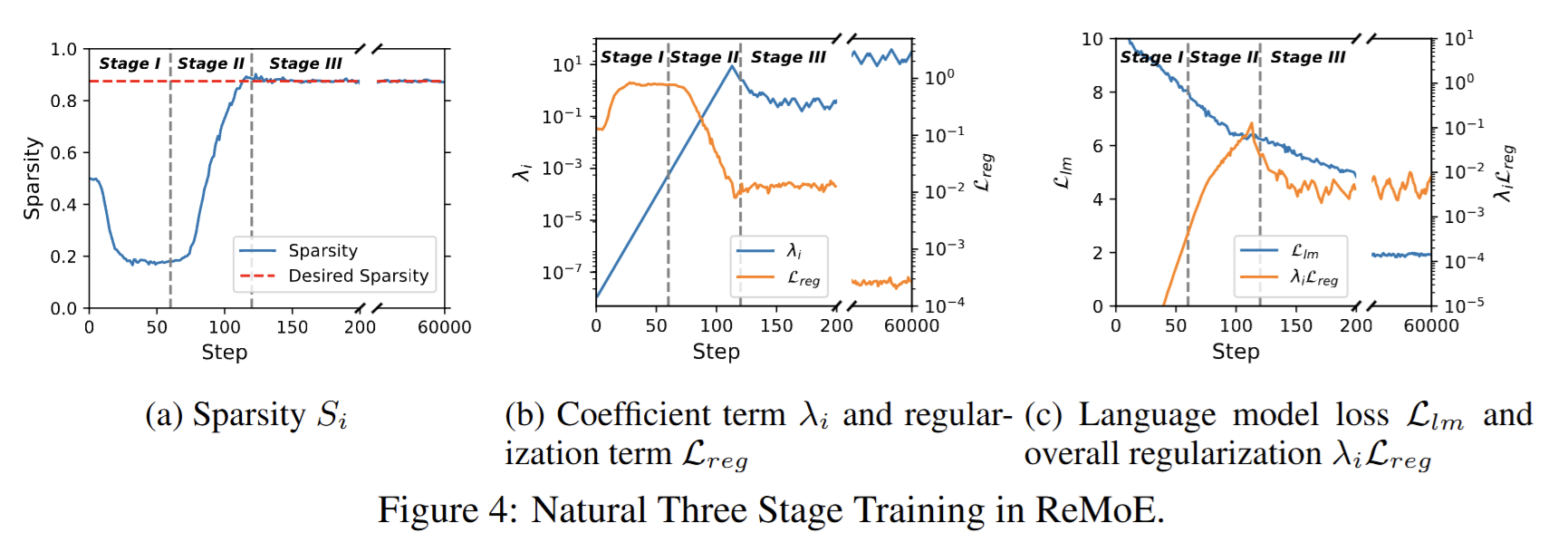
The first stage is the warm-up stage, or the dense stage. During this stage, ${\lambda }_i$ is small, while $L_{lm}$ is large and decreases rapidly. Training $\text{ReMoE}$ at this stage is nearly equivalent to training its dense counterpart with the same total number of parameters. Each expert processes more than half of the tokens, allowing the experts to diversify from their random initializations.

The second stage is the sparsifying stage, or the dense to sparse stage. At this point, the sparse regularization term ${\lambda }_i$ $L_{reg}$ becomes significant, causing the $\text{ReLU}$ routers to activate fewer experts. This forces the experts to become more diverse without causing an increase in $L_{lm}$

The third stage is the stable stage, or the sparse stage. In this phase, the sparsity $S_i$ stabilizes at the preset target. During this stage, $L_{lm}$ is optimized while being softly guided along the sparse subspace by $L_{reg}$ . Both $L_{reg}$ and ${\lambda }_i$ change very slowly, with $L_{reg}$ gradually decreasing and ${\lambda }_i$ gradually increasing. However, the overall regularization term, ${\lambda }_i$ $L_{reg}$ , remains relatively constant.

Results

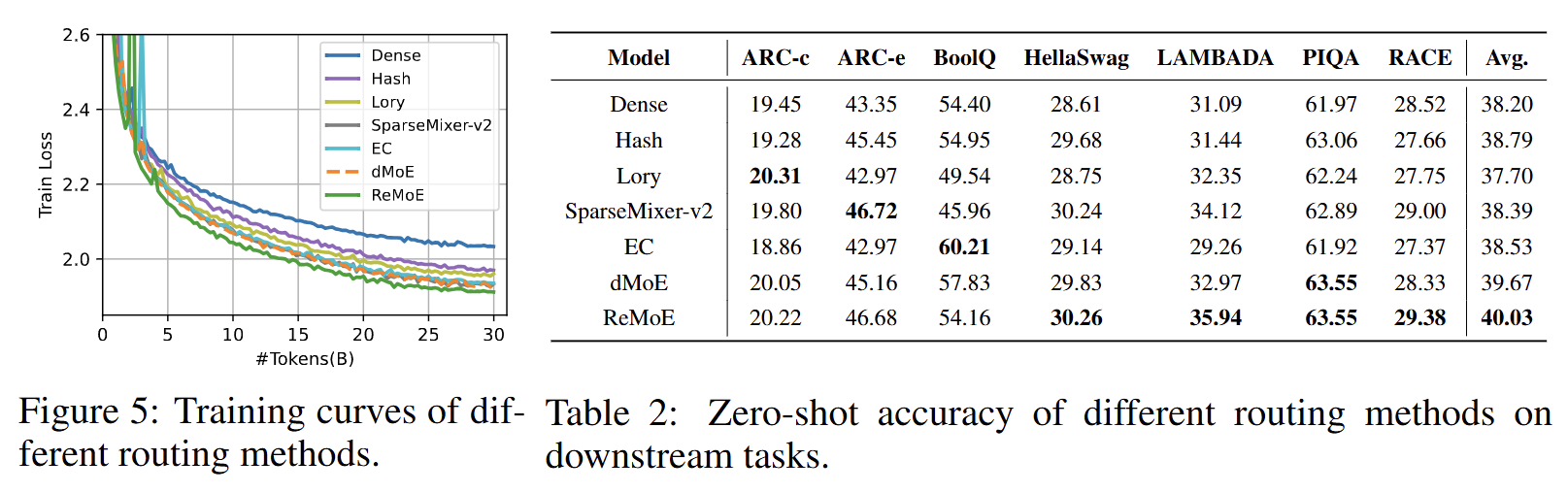
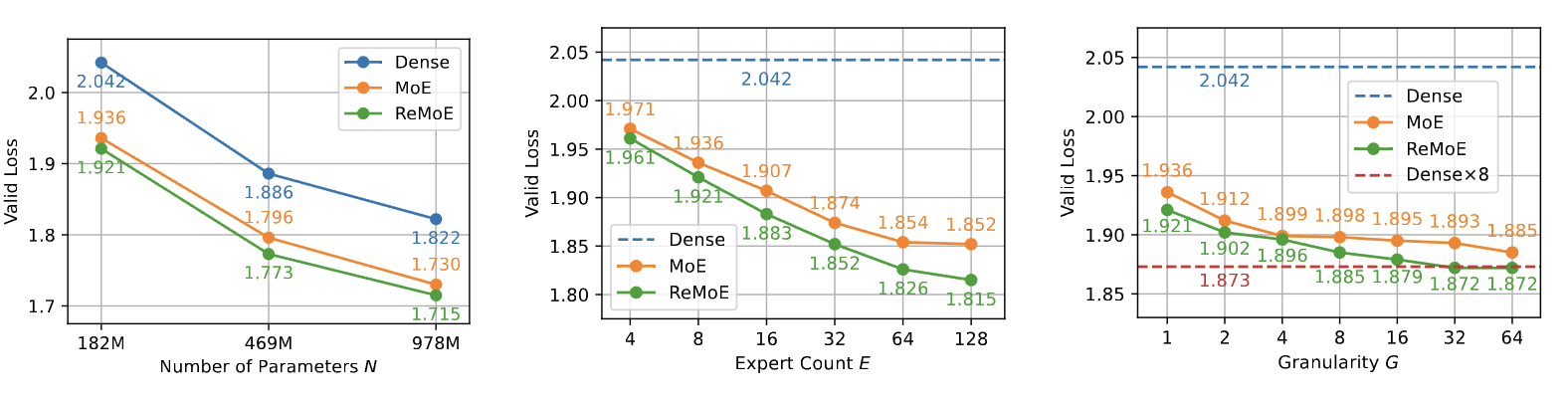
The authors perform extensive testing. They provide many details and it should be fairly easy to replicate.

Discussion

Dynamic expert allocation

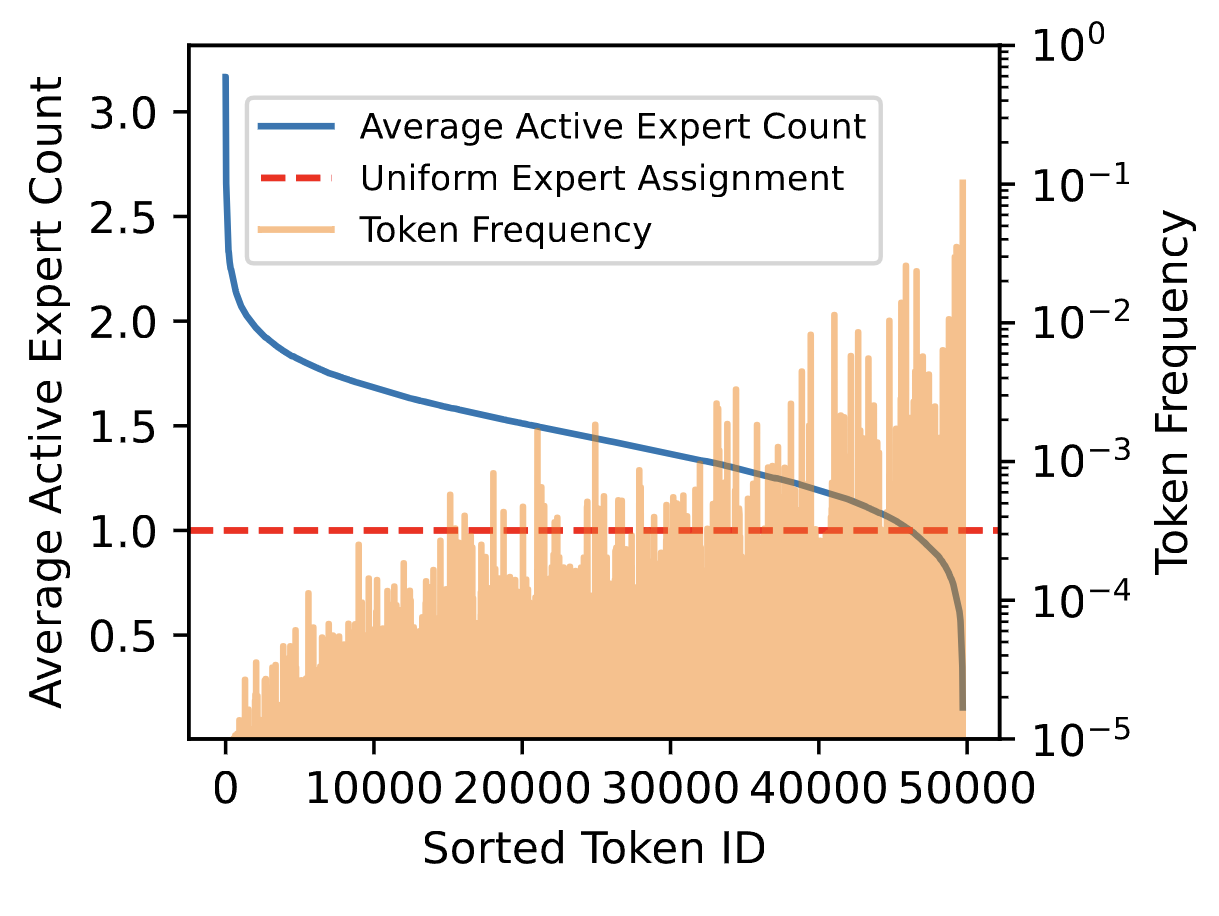
Authors claim that model dynamically allocates compute in prediction of common vs rare tokens.

Role of load balancing

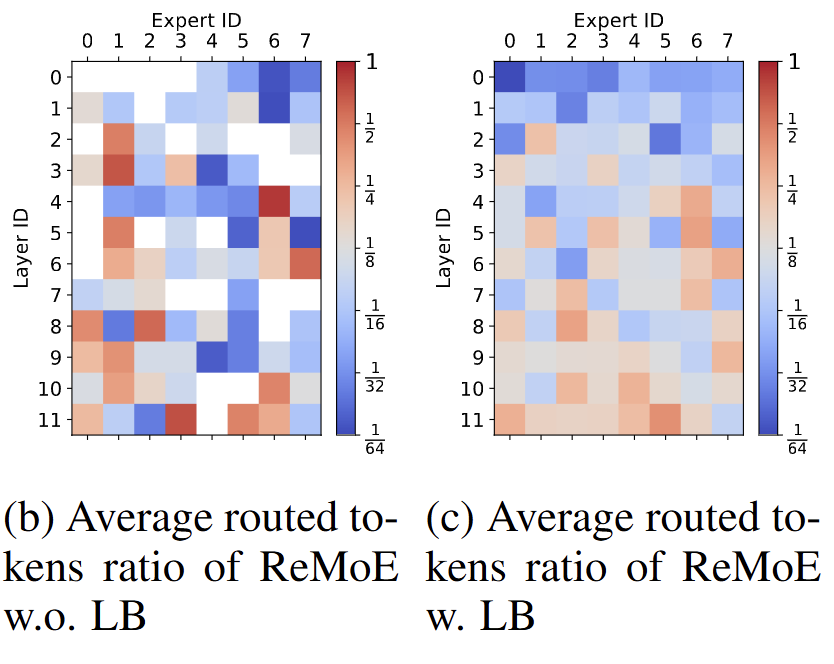
The white boxes are the experts which were activated with fewer than $\frac{1}{64}$ tokens. It’s interesting how very few experts are needed in the earlier layers when compared to the later layers.

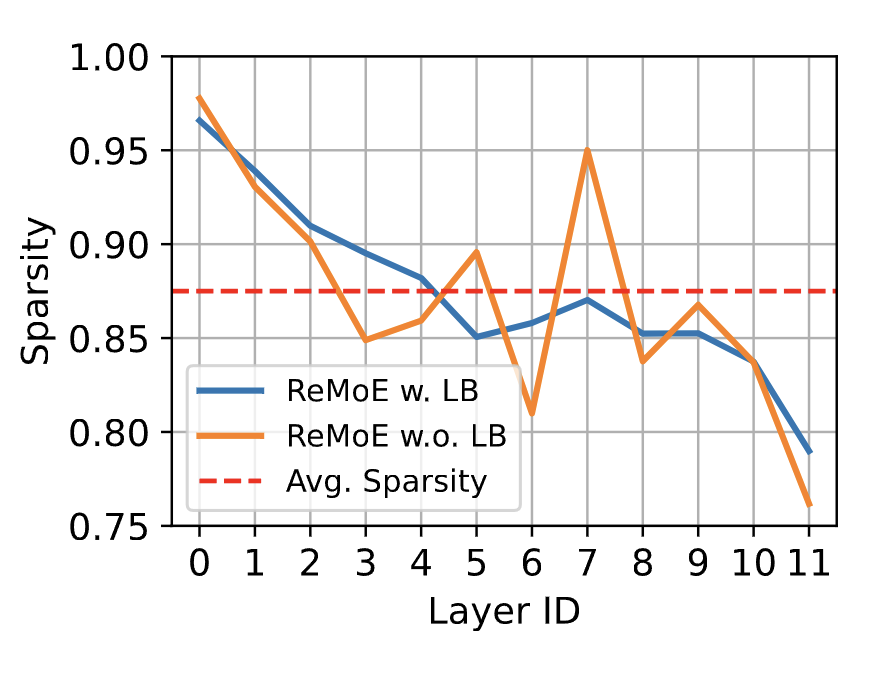
Average sparsity is around the desired level but earlier layers are so sparse when compared to later layers.

Domain specialised experts

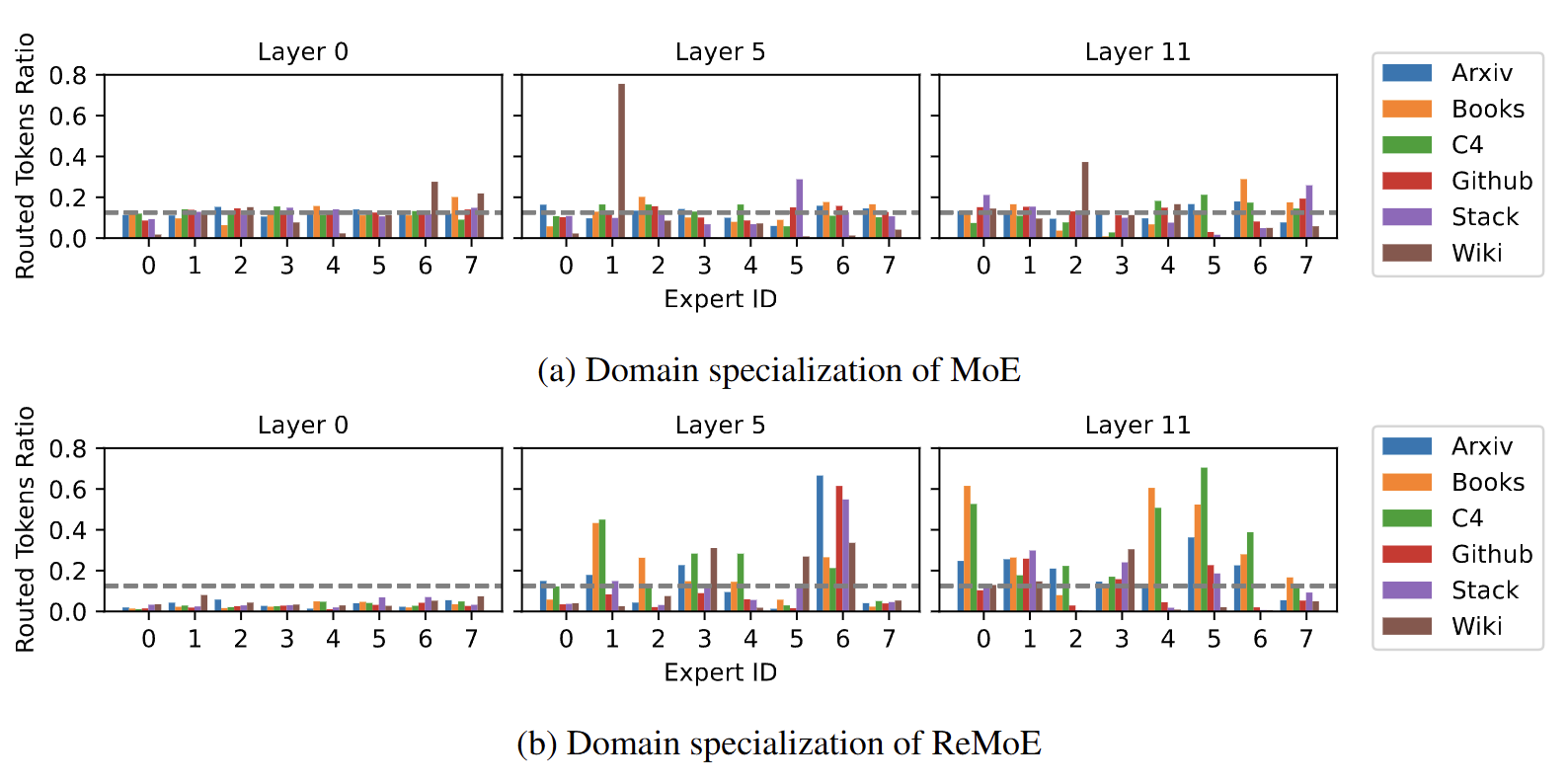
Also the experts are specialised when compared to regular $\text{Top-k}$