Identity Mappings in Deep Residual Networks

Paper: arxiv
Authors: Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Date of Publication: 16th March 2016

This paper was in the Ilya Sutskever’s 30 papers to read list. That is where I found it. Authored by the famous Kaiming.

Deep Residual Networks

Deep Residual units are defined as:

$$\begin{gathered} y_l=h({\mathbf{x}}_l)+\mathcal{F}({\mathbf{x}}_l,W_l) \\ {\mathbf{x}}_{l+1}=f(y_l) \end{gathered}$$

where $x_l$,$x_{l+1}$ are the input and output of the $l^{th}$ unit. And $\mathcal{F}$ is a residual function. If $h({\mathbf{x}}_l)$ is an identity, and $f$ is ReLU, then it is a classic Residual block as in the Resnet paper.

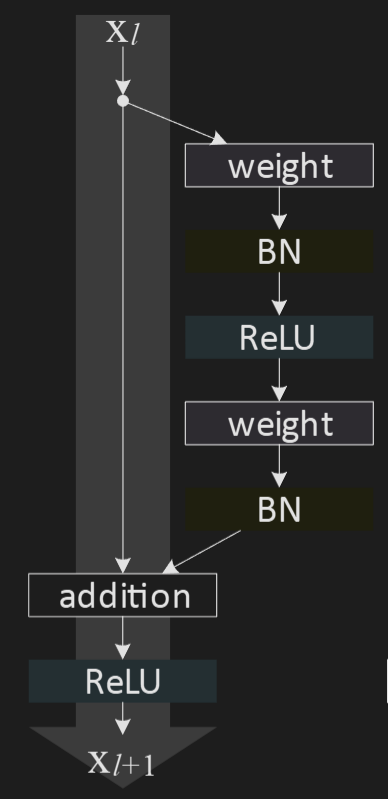
Analysis of Deep Residual Networks

ReLU function in the above image is $f$. Notice that, if $f$ was an identity function too (note that $h$ is anyway identity as defined in the Resnet paper), then we can substitute the equation for $y_l$ from above in ${\mathbf{x}}_{l+1}=f(y_l)$ and get:

$${\mathbf{x}}_{l+1}=x_l+\mathcal{F}({\mathbf{x}}_l,W_l)$$

Recursively doing it, for any layer $L$ and $l$ (where $L$ is deeper than $l$), we’ll have:

$${\mathbf{x}}_L={\mathbf{x}}_l+\sum _{i=l}^{L-1}\mathcal{F}({\mathbf{x}}_i,W_i)$$

This form exhibits some nice properties. The feature ${\mathbf{x}}_L={\mathbf{x}}_0+{\sum }_{i=0}^{L-1}\mathcal{F}({\mathbf{x}}_i,W_i)$, of any deep unit $L$, is the summation of the outputs of all preceding residual functions plus $x_0$. This is in contrast to a regular network where $x_L$ is a ${\prod }_{i=0}^{L-1}{W}_i{\mathbf{x}}_0$ (ignoring activation functions and normalizations)

Let $\mathcal{E}$ be the loss function. Then during backpropagation, using chain rule we get,

$$\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_l}=\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_L}\frac{\partial {\mathbf{x}}_L}{\partial {\mathbf{x}}_l}=\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_L}\left(1+\frac{\partial }{\partial {\mathbf{x}}_l}\sum _{i=l}^{L-1}\mathcal{F}({\mathbf{x}}_i,W_i)\right)$$ $$=\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_L}+\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_L}\frac{\partial }{\partial {\mathbf{x}}_l}\sum _{i=l}^{L-1}\mathcal{F}({\mathbf{x}}_i,W_i)$$

This consists of two terms. A term directly propagates information from layer $L$ to layer $l$ directly without concerning any middle layers and another term that propagates through middle layers.
The term also ensures that the gradients do not vanish even when the weights in the middle layers are arbitrarily small.

Let us suppose $h({\mathbf{x}}_l)={\lambda }_l{\mathbf{x}}_l$. Then:

$${\mathbf{x}}_{l+1}={\lambda }_l{\mathbf{x}}_l+\mathcal{F}({\mathbf{x}}_l,W_l)$$

The backpropagation equation would then become:

$$\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_l}=\frac{\partial \mathcal{E}}{\partial {\mathbf{x}}_L}\left(\left(\prod _{i=l}^{L-1}{\lambda }_i\right)+\frac{\partial }{\partial {\mathbf{x}}_l}\sum _{i=l}^{L-1}\hat{\mathcal{F}}({\mathbf{x}}_i,W_i)\right)$$

If ${\lambda }_i>1$ for all $i$, then ${\prod }_{i=l}^{L-1}{\lambda }_i$ will be exponentially large in a very deep network. And if ${\lambda }_i<1$, then it would be exponentially small. We would face the explosion and vanishing of the gradient respectively.

Experiments on Skip Connections

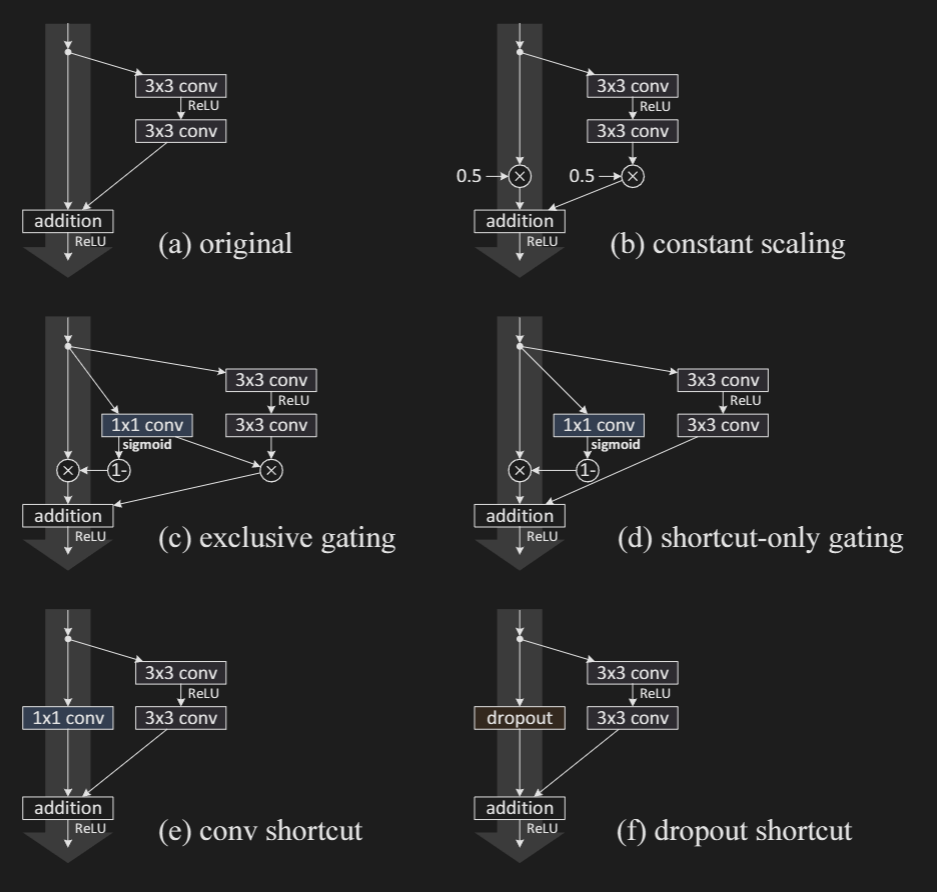
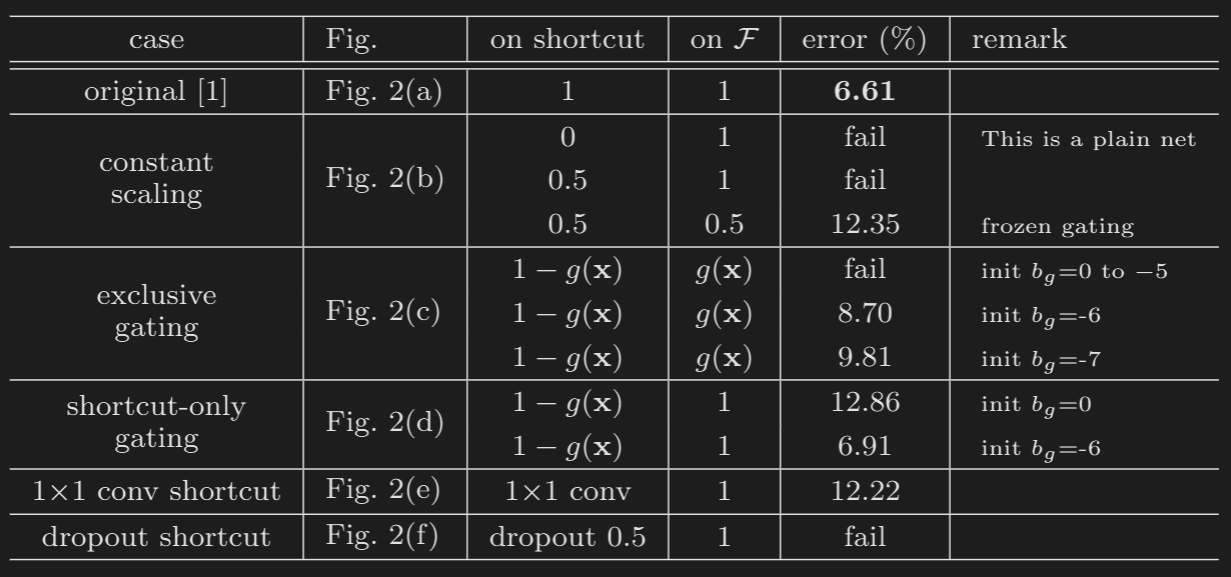
Constant Scaling: In the case of Constant scaling, we simply multiply with ${\lambda }_i$ as described above. The results are in the above table.

Exclusive Gating: We consider a gating function, $g(\mathbf{x})=\sigma (W_g\mathbf{x}+b_g)$ where $\sigma$ is a sigmoid. As seen in the above figure (c), the $\mathcal{F}$ path is scaled by $g(x)$ and the shortcut path is scaled by $1-g(x)$.
When $1-g(x)$ approaches $1$, the gated shortcut connection is closer to identity, which the gated shortcut connections are closer to identity which helps information propagation; but in this case $g(x)$ approaches $0$ and suppresses the function $\mathcal{F}$.

Short-cut only gating: In this case the path $\mathcal{F}$ is not scaled and only the shortcut is path is sclaed by $1-g(x)$, where $g(\mathbf{x})=\sigma (W_g\mathbf{x}+b_g)$. The initialized value of $b_g$ is crucial in this case. When it is initialized to $0$, the initial expectation of $1-g(x)$ is $0.5$ (as expectation of $g(x)$ is $0.5$ as it is passed through a sigmoid). The network converges to a poor result of 12.86 error percent.
But if $b_g$ is very negatively biased ($-6$ in this case), the value of $(1-g(x))$ is much closer to $1$, preserving the identity mapping. We see the result closer to the baseline Resnet-110 with error percentage of $6.91$.

Dropout: Dropout on the shortcut statistically imposes a scale of $\lambda$ with expectation of $0.5$. Thus, we see a vanishing of gradient, and it fails to learn.

Experiments on Activation Functions

Throughout this section, this is considered as the original resnet block as presented in the original paper.

As theorised (and also seen in the earlier experiments), we need an identity mapping for $f$. Before doing that, authors perform a few more experiments.

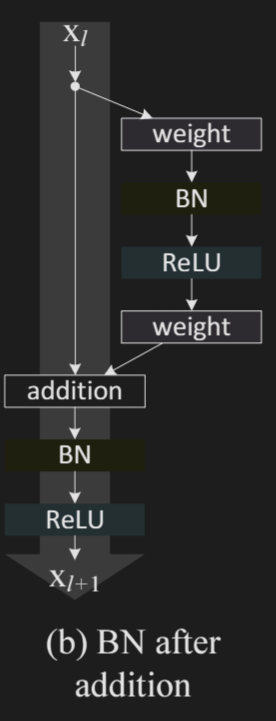
BN after addition

Authors use a batchnorm before addition as can be seen in the image. The resulting model performs worse than the baseline as batchnorm impedes signal.

ReLU before addition

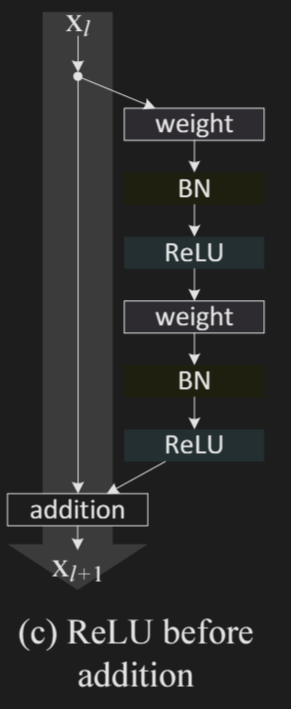
By having a ReLU on the output of $\mathcal{F}$, we make the output strictly non-negative. As a result, the signal is monotonically increasing through the layers. This hurts the performance.

Post-activation vs pre-activation

Original architecture has an activation function post the addition of shortcut to the output of $\mathcal{F}$. From the flow of gradient that we have derived above, we can clearly see that having a ReLU post addition is not optimal.
So, instead of using the activation function on the skip-connection too, authors use an activation function asymetrically, only in $\mathcal{F}$. Thereby, the skip-connection is just an identity, without any activations on its way, and the above derived flow of the gradient holds.

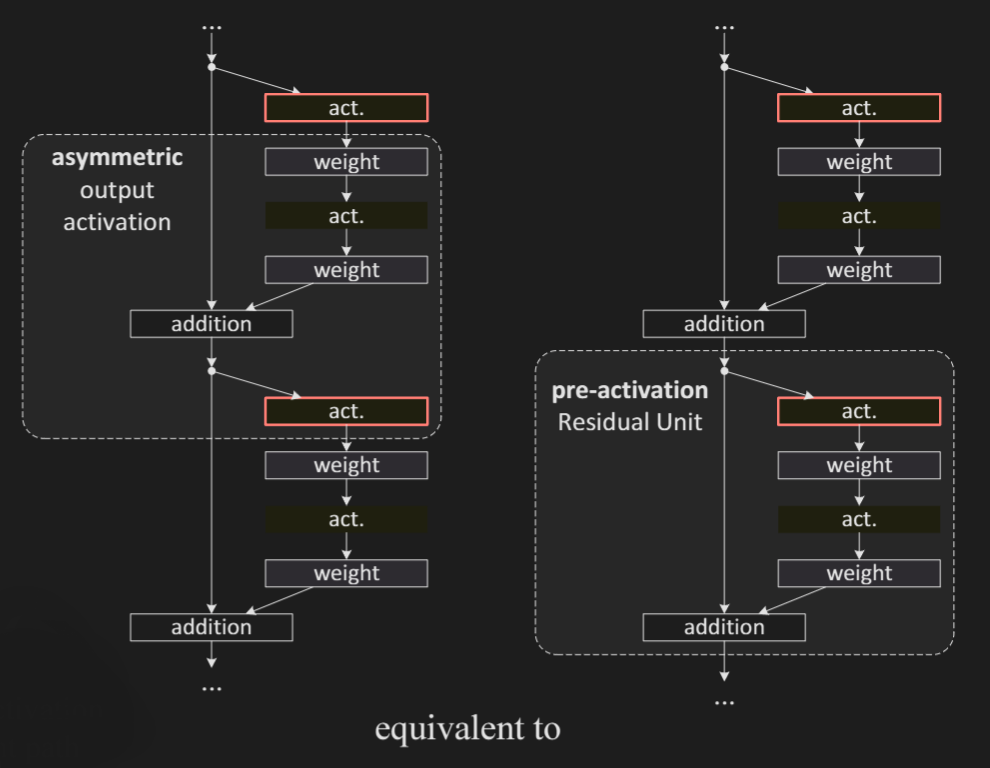
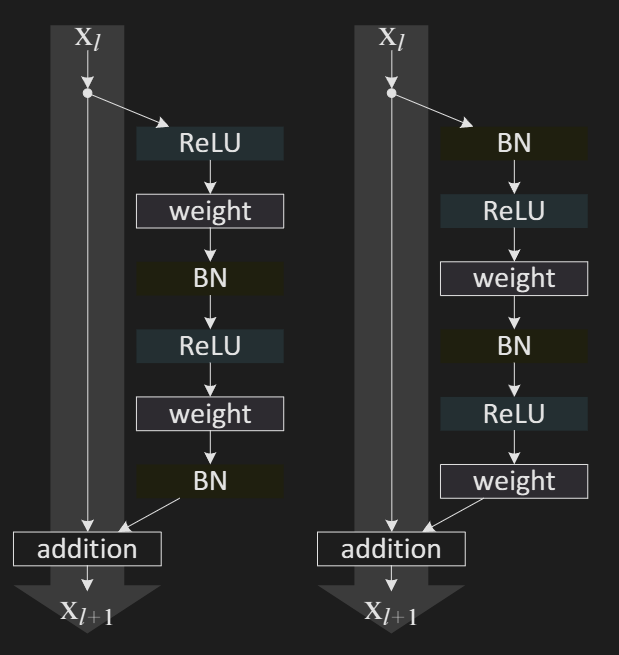
Authors experiment with two such designs: (i) ReLU-only pre-activation, and (ii) full pre-activation where BN and ReLU are both adopted before weight layers. Results show that adopting both BN and ReLU leads to a better performance.

The newly proposed modification beats the original Resnet architecture.

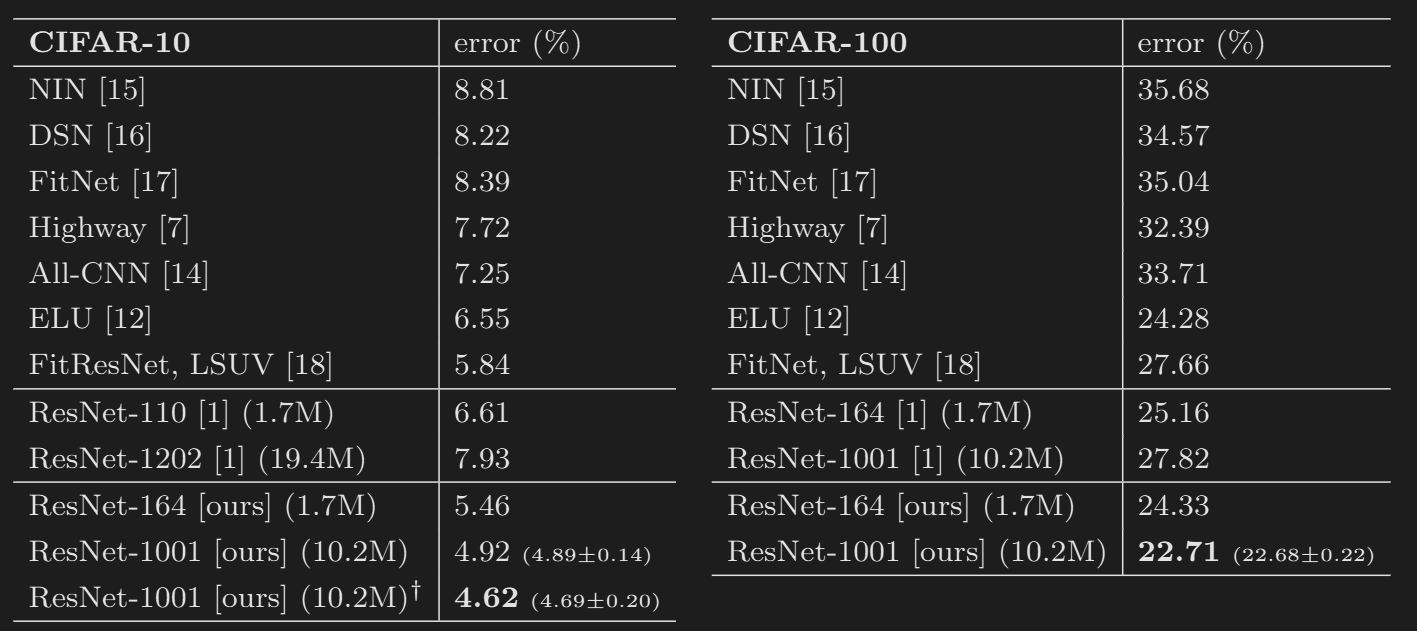
Authors manage to train a Resnet-1001 with this modification. This new varient is easier to train.
They also claim that it helps in regularization and helps achieve a higher test-loss. Regularization is due to BN’s regularization effect. In the original design, after batch-norm, $\mathcal{F}$ is immediately added to the shortcut and the resultant signal is not normalized. The new modification fixes that issue.